三角函数

$$
sin^2x + cos^2x = 1\\
six(x + y) = sinxcosy + conxsiny\\
cos(x + y) = cosxcosy - sinxsiny\\
sinx = \sum_{n=0}^{\infty}\frac{(-1)^{n}x^{2n+1}}{(2n+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ...\\
cosx = \sum_{n=0}^{\infty}\frac{(-1)^{n}x^{2n}}{(2n)!} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ...
$$

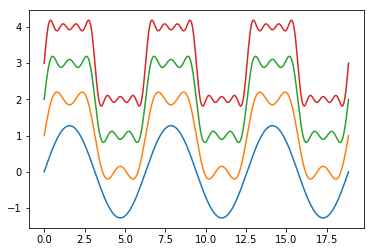
正弦信号合成方波信号

通过python绘制下述正弦信号的波形图：
$$
\frac{4sin\theta}{\pi} + \frac{4sin3theta}{3\pi} + \frac{4sin5\theta}{5\pi} + \frac{4sin7\theta}{7\pi}
$$

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 6 * np.pi, 1000, endpoint=True)
z = (4 * np.sin(x)) / (np.pi)
z1 = 1 + (4 * np.sin(x)) / (np.pi) + (4 * np.sin(3 * x)) / (3 * np.pi)
z2 = 2 + (4 * np.sin(x)) / (np.pi) + (4 * np.sin(3 * x)) / (3 * np.pi) + (4 * np.sin(5 * x)) / (5 * np.pi)
z3 = 3 + (4 * np.sin(x)) / (np.pi) + (4 * np.sin(3 * x)) / (3 * np.pi) + (4 * np.sin(5 * x)) / (5 * np.pi) + (4 * np.sin(7 * x)) / (7 * np.pi)

plt.plot(x, z)
plt.plot(x, z1)
plt.plot(x, z2)
plt.plot(x, z3)

plt.show()

结果：

卷积

卷积定理指出，函数卷积的傅里叶变换是函数傅里叶变换的乘积。即一个域中的卷积对应于另一个域中的乘积，例如时域中的卷积对应于频域中的乘积。
$$
\int_{ -\infty}^{\infty}f(\tau)(x-\tau)dx
$$
使用numpy模块进行卷积运算，通过卷积计算杨辉三角。

# -*- coding: utf-8 -*-
import numpy as np

x = np.array([1, 1])
y = np.array([1, 1])
xx = 0
while xx < 10:
    print (y)
    y = np.convolve(x, y)
    xx = xx + 1

欧拉公式

$$
x = cos\, \omega_0t + jsin\, \omega_0t = e^{j\omega_0t}
$$

由欧拉公式可以推出：
$$
cos\,wt = \frac{e^{jwt} +e^{-jwt}}{2}\\
sin\,wt = \frac{e^{jwt}-e^{-jwt}}{2j} = -\frac{j}{2}(e^{jwt}-e^{-jwt})
$$

傅里叶级数

$$
f(t) = \frac{a_0}{2} + \sum_{k=1}^{\infty}(a_kcos\,k{\omega}_0t + b_ksin\,k{\omega}_0t) \\
其中：\\
\omega_0 = \frac{2{\pi}}{2}\\
a_k = \frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)cos\,k{\omega}_0t\,dt (k = 0, 1, 2, ...)\\
b_k = \frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)sin\,k{\omega}_0t\,dt (k = 1, 2, ...)
$$

周期函数$f(x)​$可以分解为：

• 直流分量$(\frac{a_0}{2})$
• 余弦分量$(a_kcos\,k\omega_0t)$
• 正弦分量$(b_ksin\,k\omega_0t)$

复指数形式的傅里叶级数

$$
f(t) = \frac{a_0}{2} + \sum_{k=1}^{\infty}(a_kcos\,k{\omega}_{0}t + b_ksin\,k{\omega}_0t)\\
= \frac{a_0}{2} + \frac{1}{2}\sum_{k=1}^{\infty}(a_k(e^{kj\omega_0t} + e^{-kj\omega_0t}) - jb_k(e^{kj\omega_0t} - e^{-kj\omega_0t}))\\
= \frac{a_0}{2} + \frac{1}{2}\sum_{k=1}^{\infty}[(a_k-jb_k)e^{kj\omega_0t} + (a_k + jb_k)e^{-kj\omega_0t})]\\
=\frac{a_0}{2} + \frac{1}{2}\sum_{k=1}^{\infty}[(a_k-jb_k)e^{kj\omega_0t}] + \frac{1}{2}\sum_{k=1}^{\infty} [(a_k + jb_k)e^{-kj\omega_0t})]\\
= \sum_{k=0}\frac{a_k}{2} + \sum_{k=1}^{\infty}[\frac{1}{2}(a_k - jb_k)e^{kj\omega_0t} + \sum_{k=-1}^{-\infty}[\frac{1}{2}(a_{-k} + jb_{-k})e^{kj\omega_0t}]\\
= \sum_{-\infty}^{\infty}c_ke^{kj\omega_0t}
$$

因此：
$$
f(t) = \sum_{-\infty}^{\infty}c_ke^{kj\omega_0t}
$$
其中：
$$
c_k =
\begin{equation}
\left{
\begin{array}{lr}
\frac{a_0}{2}, \quad k = 0 \\
\frac{1}{2}(a_k - jb_k), \quad k = 1, 2, ... \\
\frac{1}{2}(a_{-k} + jb_{-k}), \quad k = -1, -2, ...
\end{array}
\right.
\end{equation}
$$